Understanding Binary Numbers
Base 10 vs Base 2
Binary is the language of computers. While we usually count using the decimal system (base 10), computers use the binary system (base 2). Understanding how each system works will help you make sense of digital data.
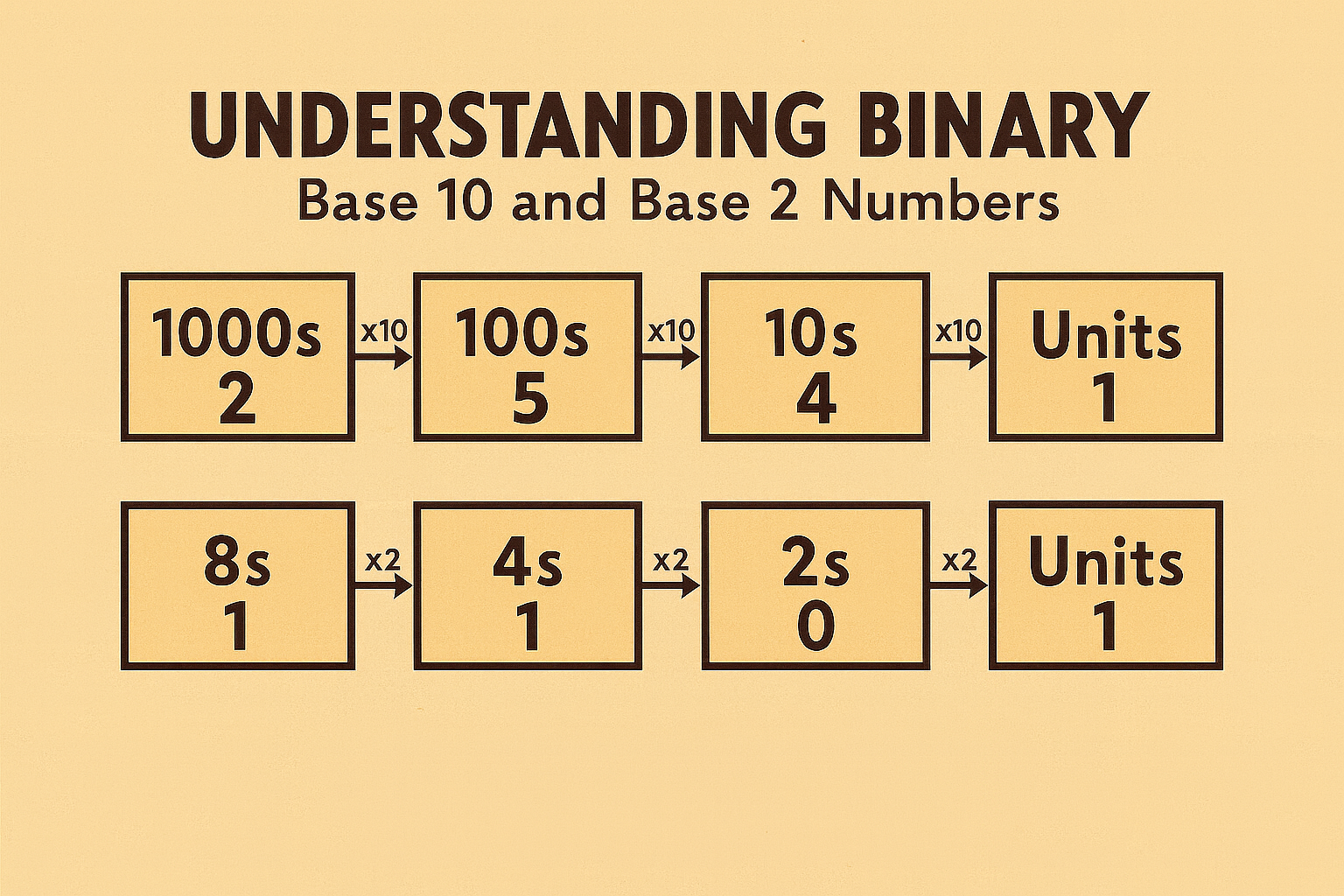
- Decimal system (base 10): uses ten digits (0–9). Each place value is ten times the one to its right.
- Binary system (base 2): uses only two digits (0 and 1). Each place value is double the one to its right.
The diagram below compares the place values of base 10 and base 2 and shows example numbers in each system.
How to Read Binary Numbers
To convert a binary number into a decimal number, follow these steps:
- Write down the place values across the top, doubling from right to left (1, 2, 4, 8, etc.).
- Place each binary digit beneath its column.
- Multiply each digit by its column’s value.
- Add the results to obtain the decimal equivalent.
The example below shows how the binary number 1101 is converted into decimal.

1101 to decimal: 1×8 + 1×4 + 0×2 + 1×1 = 13.Try converting the following binary numbers into decimal:
0111100111001111001
Bits and Bytes
A bit is a single binary digit (0 or 1). Eight bits grouped together form a byte. Every value a computer stores—from text characters to small images—can be represented by bytes. When writing bytes, always show all eight digits (e.g., 00001101).
The diagram below illustrates the place values of an 8‑bit byte and shows the conversion of the example
byte 01101011 into decimal.

The Language of Numbers
Decimal numbers have names like “ten” or “eleven,” but binary numbers are read digit by digit.
For example, the binary number 11 (spoken as “one one”) is not “eleven” — it equals 3 in
decimal.
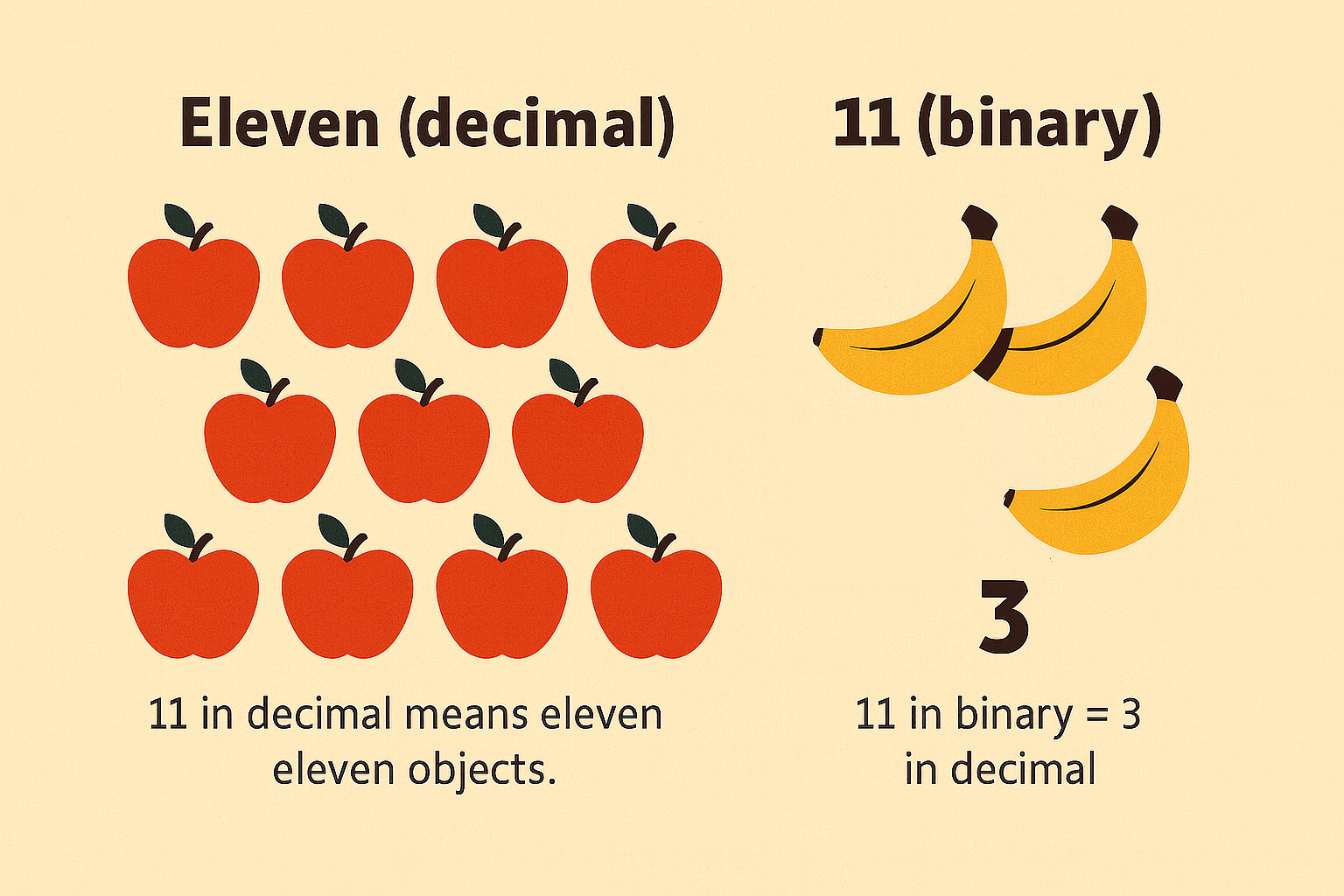
11
represents three.Binary to Decimal Shortcut
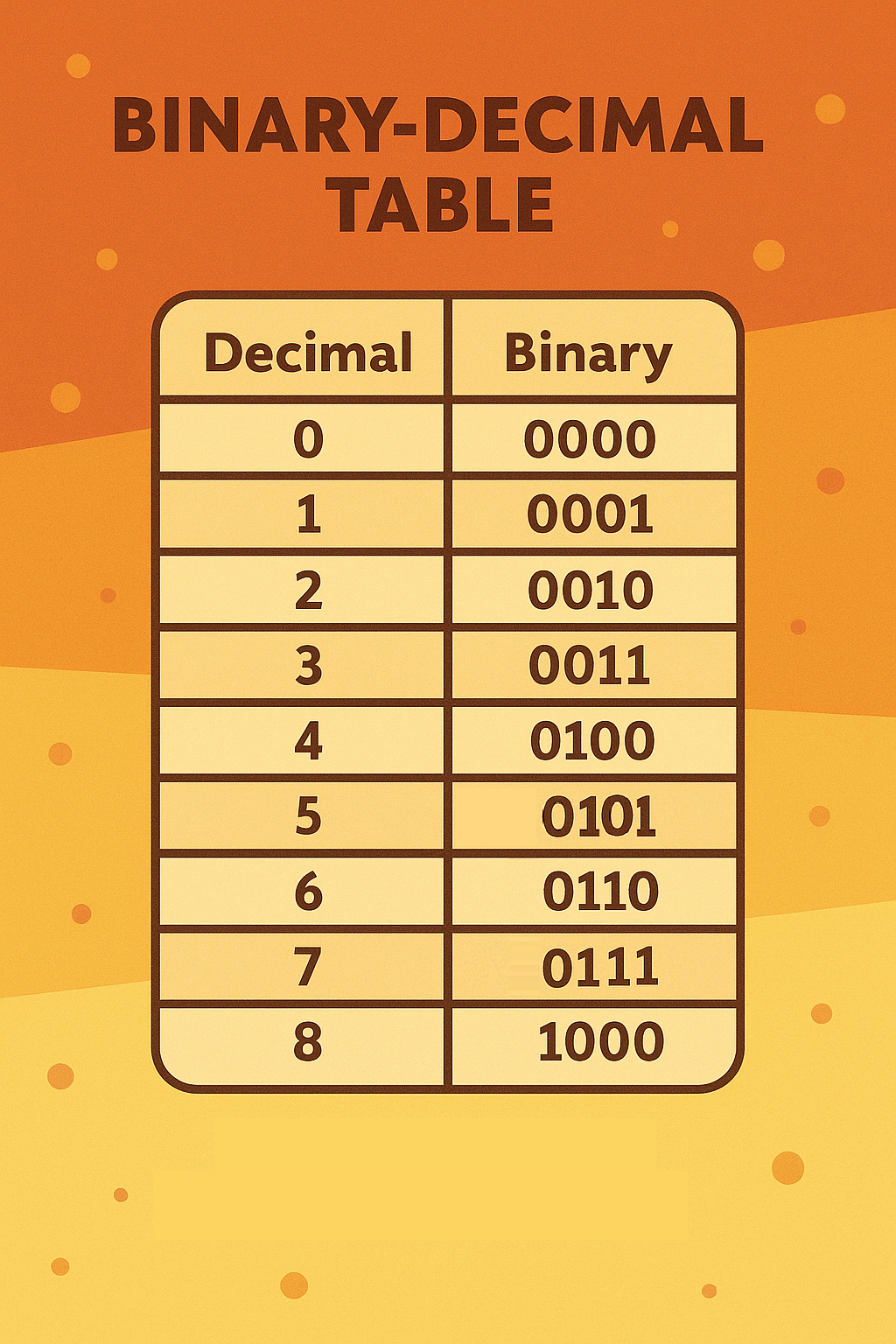
The table below lists the decimal numbers 0–9 and their corresponding 4‑bit binary representations.
Activities and Challenges
- Write the binary representations of the numbers 0–9 in order.
- Create flashcards with different binary numbers and practise arranging them with their place‑value headings.
- Quiz yourself or a friend on converting binary numbers like
1001or110011into decimal. - Explain why the 1 in the binary number
00010000sits in the 2⁴ column. - Describe what “base 2” means and how it differs from base 10.
